| 年级 | 科目 | 问题描述 | 提问时间 |
| 初二 | 数学 | 二次根式 | 2014-02-26 21:02:28 |
如图,在矩形ABCD中,CE⊥BD,E为垂足,连结AE,已知AB=a,BC=1,求△AED的面积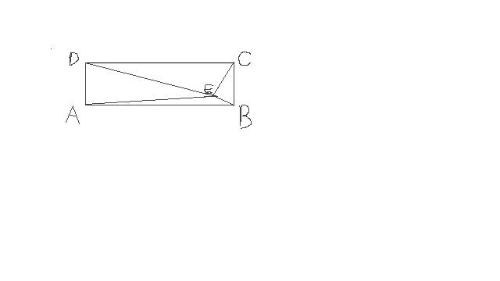 | |||
| 王老师 2014-02-27 09:34:09 | |||
解: ∵矩形ABCD,AB=A,BC=1 ∴AD=BC=1,CD=AB=a ∴BD=√(AD²+AB²)=√(1+ a²) ∵CE⊥BD ∴BD*CE/2=CD*BC/2 ∴CE=CD*BC/BD=a/√(1+ a²) ∴BE²=BC²-CE²=1- a²/(1+ a²)=1/(1+ a²) ∴BE=1/√(1+ a²) ∴DE=BD-BE=√(1+ a²)-1/√(1+ a²)=a²/√(1+ a²) ∴DE/BE=[a²/√(1+ a²)]/[ 1/√(1+ a²)]=a² ∵△ADE、△ABE等高 ∴S△ADE/ S△ABE=DE/BE=a² ∵S△ABD=AB*AD/2=a/2 ∴S△ADE=a/2* a²/(1+ a²)=a^3/2(1+ a²) | |||