| 年级 | 科目 | 问题描述 | 提问时间 |
| 高一 | 数学 | 数学 | 2014-04-26 20:46:21 |
 | |||
| 王老师 2014-04-26 21:10:07 | |||
解:
n=1时,2a1-a1=a1=S1S1=a1²
a1²-a1=0 a1(a1-1)=0
a1=0(舍去)或a1=1
n≥2时,2an-a1=2an-1=S1Sn=Sn
Sn=2an -1
an=Sn-S(n-1)=2an-1-2a(n-1)+1=2an-2a(n-1)
an=2a(n-1) an/a(n-1)=2,为定值,数列{an}是以1为首项,2为公比的等比数列。
an=1×2^(n-1)=2^(n-1)
n=1时,a1=2^0=1,同样满足通项公式,数列{an}的通项公式为an=2^(n-1)
a2=2^1=2
nan=n×2^(n-1)
Tn=1×1+2×2+3×2²+...+n×2^(n-1)
2Tn=1×2+2×2²+...+(n-1)×2^(n-1)+n×2ⁿ
Tn-2Tn=-Tn=1+2+...+2^(n-1)-n×2ⁿ
=1×(2ⁿ-1)/(2-1)-n×2ⁿ
=(1-n)×2ⁿ -1
Tn=(n-1)×2ⁿ +1 | |||
| 王老师 2014-04-26 21:43:27 | |||
 | |||
| 王老师 2014-04-26 21:43:39 | |||
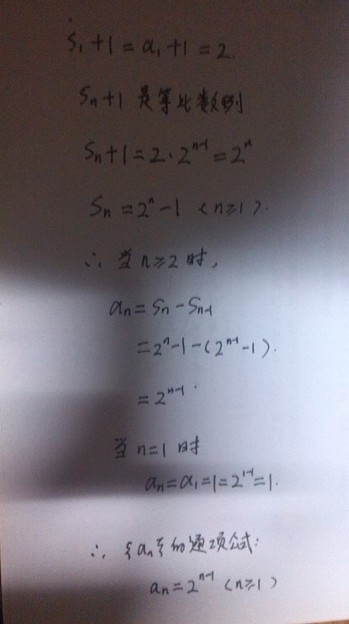 | |||
| 王老师 2014-04-26 21:43:52 | |||
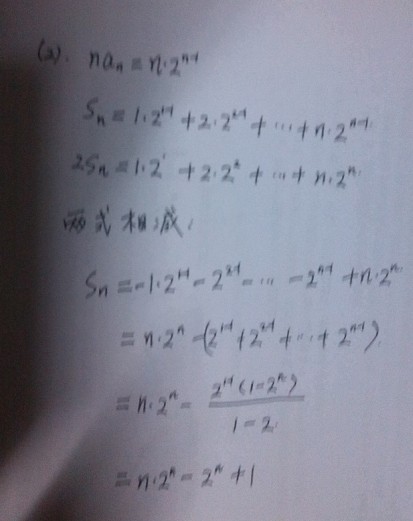 | |||