学点点

详细内容

疑难解答：

学员在学习中遇到问题，在这里能得到及时的解决。有问题随时提问，老师解答及时，不留学习盲点。有不懂的题目问老师，逐渐养成独立解决问题的能力。

年级

科目

问题描述

提问时间

初二

数学

2014-05-11 14:35:15

王老师 2014-05-11 14:41:37

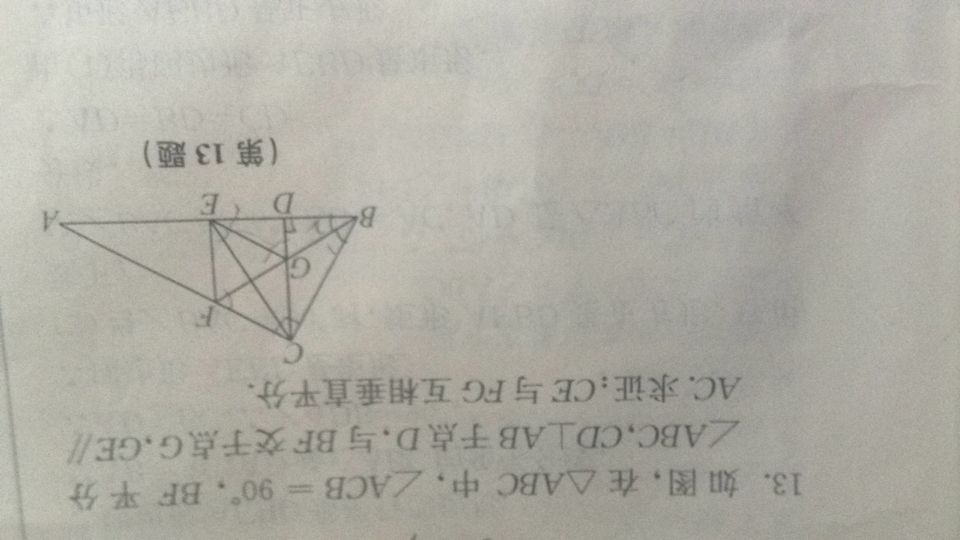
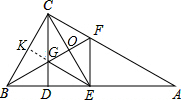
证明：延长EG交BC于点K．
∵GE∥AC，∠ACB=90°，
∴∠BKE=∠ACB=90°，即EK⊥BC．
又∵CD⊥AB，BF平分∠ABC，
∴GK=GD．
在Rt△GKB与Rt△GDB中，

GK＝GD

BG＝BG

，
∴Rt△GKB≌Rt△GDB（HL），
∴DB=BK．
在△CBD与△EBK中，

∠CBD＝∠EBK

BD＝BK

∠CDB＝∠EKB

，
∴△CBD≌△EBK（ASA），
∴BC=BE，
∴BF垂直平分CE（三合一）．
∴CO=EO，
在△COF与△EOG中，

∠FCO＝∠GEO

CO＝EO

∠COF＝∠OG

，
∴△COF≌△EOG（ASA）
∴FC=GE，
又∵GE∥AC．
∴四边形FCGE为平行四边形，
∵CG=GE，
∴四边形FCGE为菱形，
∴CE与GF互相垂直平分

王老师 2014-05-11 14:42:01

该问题已结帖